写给大家看的 Lambda 演算

Sep 08, 2022

An introduction to Lambda calculus

Slide: https://talks.yhj.me/lambda-calculus

What is Lambda calculus

λ 演算是一个形式化的数学逻辑系统，它由数学家阿隆佐·邱奇在 20 世纪 30 年代首次发表。它基于函数的抽象和应用，使用变量绑定和替换来表示计算。 λ 演算作为一种广泛用途的计算模型，可以清晰地定义什么是一个可计算函数，而任何可计算函数都能以这种形式表达和求值，它能模拟单一磁带图灵机的计算过程；尽管如此，λ 演算强调的是变换规则的运用，而非实现它们的具体机器。

推荐大家阅读以下两篇博文，作者用便当盒模拟了 Lambda 演算:

Terms

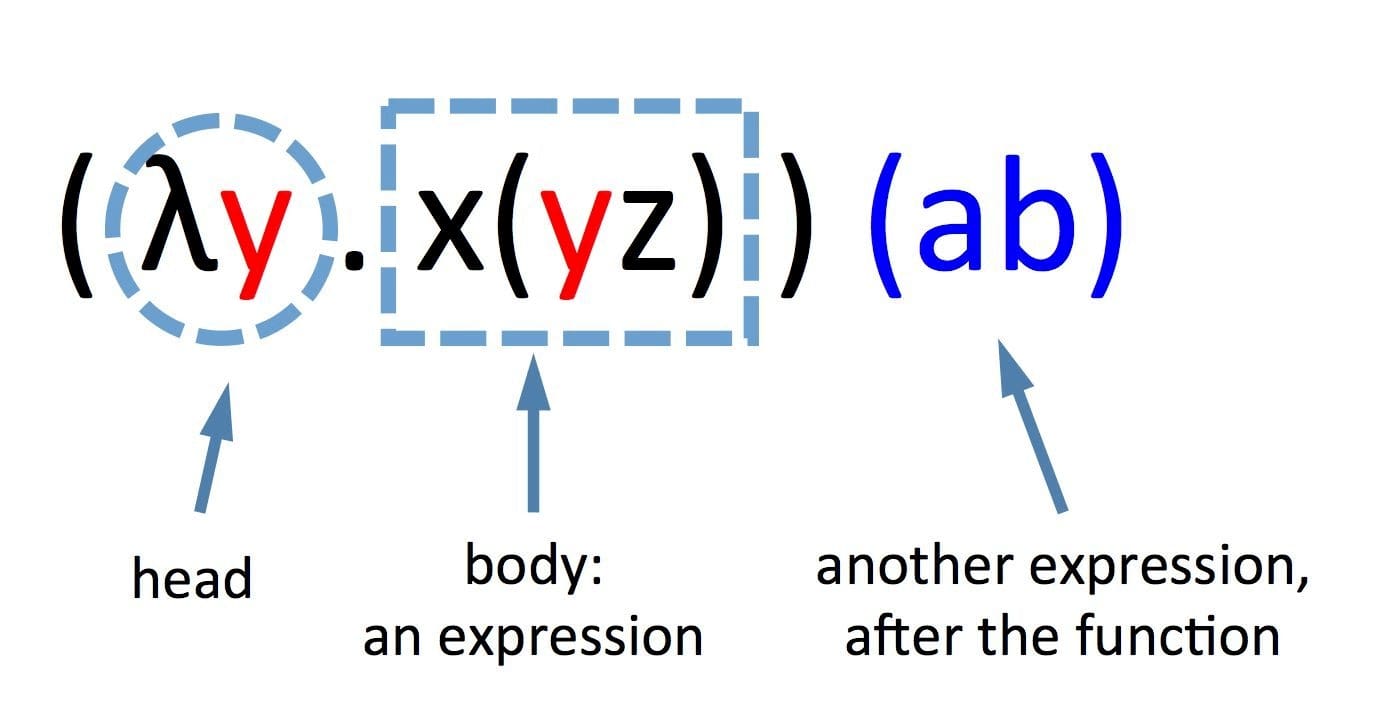
语法	名称	例子	说明
<name>	变量	x	名称为 x 的变量
λ<parameters>.<body>	抽象，也就是函数	λx.x	一个完整的函数定义, 形参为x, 函数体为 x.
<function> <variable or function>	应用	M N	将函数 M 作用于参数 N

Variables

在 λx.x y 中，其中 x 是绑定变量(Bound Variable)，y 是自由变量(Free Variable)。自由变量也就意味着和表达式的上下文无关。一个不包含自由变量的表达式被称为是封闭的(closed)。封闭的 λ 表达式也称为组合子(Combinator)。部分标准组合子的名称可以参考维基百科。

Operations

α-conversion

Alpha 变换，在 λ 演算中，变量名称是无关紧要的。例如 λx.x 和 λy.y 是等价的。

λx.x = λy.y

在 λ 表达式中都习惯用单个字母来命名变量，经过一些规约后，在不同的项当中容易重名导致歧义。例如 λx.x.(λx.λy.y x) x 中蓝色的变量 x 和橙色的变量 x 其实是两个不同的变量，于是我们就可以通过 α 变换将其中一个 x 重命名。比如说将蓝色的 x 重命名为 z 得到 λz.(λx.λy.y x) z

β-reduction

Beta 规约，用实参替换函数中的形参，也就是对函数求值的过程。

(λx.x) y // β: (λx.x) y -> x[x := y] = y   // beta 规约的表示形式
= y
// js
(x => x)(y)
= y
(λx.x y) a b // β: (λx.x y) a -> (x y)[x := a] = (a y)
= (a y) b
= a y b
// js
(x => x(y))(a)(b)
= (a(y))(b)
= a(y)(b)

关于求值顺序，对于 (λx.x)((λz.z) s) 这种表达式，你可以以两种顺序进行规约。

// 从内到外
(λx.x)((λz.z) s) // β: (λz.z) s -> z[z := s] = s
= (λx.x) s       // β: (λx.x) s -> x[x := s] = s
= s
// 从外到内
(λx.x)((λz.z) s) // β: (λx.x)((λz.z) s) -> x[x := (λz.z) s] = (λz.z) s
= (λz.z) s       // β: (λz.z) s -> z[z := s] = s
= s

根据 Chruch-Rosser theorem 证明这两种顺序是等价的。对应到编程语言上，前者是立即求值，后者是惰性求值。

η-reduction

对于这样的一个函数 λx.M x 将它应用于参数 N 即 (λx.M x) N，beta 规约后等于 M N，这说明 M = (λx.M x)。
对于 λx.M x，其中 M 中不包含绑定变量 x 的函数抽象，那么它是冗余的，这个过程我们叫作 eta 规约。它一般用于清除 λ 表达式中存在的冗余函数抽象。

// f2 和 f1 完全等价，所有用 f2 的地方都可以直接替换成 f1
let f1 = v => v
let f2 = n => f1(n)
f1(1) // 1
f2(1) // 1

Conventions

最外层的括号会被丢弃，M N 表示 (M N)
函数应用是左结合的，M N P 表示 ((M N) P)，用 js 描述的话即 M(N)(P) 而非 M(N(P))
一个函数抽象的函数体将尽最大可能向右扩展，λx.M N 表示的是 λx.(M N) 而不是 (λx.M) N
连续的函数抽象可以被缩写，λx.λy.λz.N 可以缩写成 λxyz.N

Curring

λ 演算中函数都是单参函数，一个需要多个参数的才能计算的表达式都需要写成高阶函数的形式。例如一个加法函数

λa.λb.+ a b  // 这里暂时用 + 号表示对两个数求和的函数
// js
const fn = a => b => a + b

通过柯里化，我们可以很容易的将一个多参函数转换成单参调用的形式，于是我们可以使用更加直观的多参函数形式来表示：λa b.+ a b。一个简易版的 js 柯里化工具函数实现也非常简单。

const curry = (f) => {
  const args = [];
  const g = (x) => {
    args.push(x)
    if (args.length >= f.length) {
      return f(...args)
    } else {
      return g
    }
  }
  return g
}
const plus = (a, b) => a + b
const curried = curry(plus)
curried(1)(2) // 3

Alias

我们可以给一个 λ 函数一个别名，在一些复杂的表达式中使用别名会更加易读和清晰。

Plus := λa.λb.+ a b // 这里暂时用 + 号表示对两个数求和的函数

Church encoding

λ 演算中只有函数，没有数字，字符串，数组等类型。丘奇编码通过函数来实现与这些数据类型的相同的行为和特征。我们只关心数据类型之间的运算，不关心它的表现形式或者说长什么样。

Church booleans

在丘奇编码中 True 和 False 其实表示的是对参数的选择。定义一个包含两个参数的函数，如果永远返回第一个参数，则表示 True。如果永远返回第二个参数，则表示为 False。

True  := λa b.a // λa.λb.a
False := λa b.b // λa.λb.b

我们观察这样的一个 js 函数。从结果上看，如果最终返回 a，则表示 condition 是 True；如果最终返回 b，则说明 condition 是 False;

(condition, a, b) => condition ? a : b

与前面那个 js 函数相对应的，我们可以这样来定义 if。

IF := λp a b.p a b // λp.λa.λb.p a b
IF True x y // alias: IF -> λp a b.p a b
= (λp a b.p a b) True x y // beta: p a b[p := True, a := x, b := y]
= True x y // alias: True -> λa b.a
= (λa b.a) x y // beta: (λa b.a) -> a[a := x, b := y] = x
= x

除此之外，我们还也可以定义与或非。

And := λp q.p q p
Or := λp q.p p q
Not := λp.p False True
Xor := λa b.a (NOT b) b
And True False // alias: And -> λp q.p q p
= (λp q.p q p) True False // beta: (p q p)[p := True, q := False] = True FALSE True
= True False True // alias: True -> λa b.a
= (λa b.a) False True // beta: a[a := False, b := True] = False
= False

Church numerals

常用的阿拉伯的数字只是其中一种表达自然数的方式，实际上还有许多种表示自然数的方式。

例如可以用 TypeScript 的数组类型的长度来表达

type Zero = []
type One = [true]
type Two = [true, true]
type Plus<A extends any[], B extends any[]> = [...A, ...B]
type Convert<T extends any[]> = T['length']
type A = Convert<Plus<One, Two>>
//   ^? type A = 3

自然数的定义可以参考皮亚诺公理。皮亚诺的这五条公理用非形式化的方法叙述如下：

0是自然数；
每一个确定的自然数a，都有一个确定的后继数a' ，a' 也是自然数；
对于每个自然数b、c，b=c当且仅当b的后继数=c的后继数；
0不是任何自然数的后继数；
任意关于自然数的命题，如果证明：它对自然数0是真的，且假定它对自然数a为真时，可以证明对a' 也真。那么，命题对所有自然数都真。

我们定义一个后继函数 S，S 接受一个自然数作为参数，返回其后继。于是有

0
1 = S(0)
2 = S(1) = S(S(0))
3 = S(2) = S(S(1)) = S(S(S(0)))
// ...

前面的代码用丘奇编码来表达是这样的

0 := λs.λz.z
1 := λs.λz.s z
2 := λs.λz.s (s z)
3 := λs.λz.s (s (s z))
// ...

在丘奇编码中，其实我们是使用 s 函数的调用次数来表达自然数。一个理解办法是将 z 作为是对于零值的命名，而 s 作为后继函数的名称。因此，0 是一个仅返回 “0” 值的函数；1 是将后继函数运用到 0 上一次的函数；

我们也可以用 js 来表达

let Zero = (s, z) => z
let One = (s, z) => s(z)
let Two = (s, z) => s(s(z))
let Three = (s, z) => s(s(s(z)))
// Helpers
let s = n => n + 1 // 后继函数
let convert = f => f(s, 0)
convert(Zero) // ZERO(s, 0) === 0
convert(One) // ONE(s, 0) === 1
convert(Two) // TWO(s, 0) === 2
convert(Three) // THREE(s, 0) === 3

Successor

接下来，我们来看看后继函数 Succ 用丘奇数是怎么表示的

Succ := λn f x.f (n f x) // λn.λf.λx.f (n f x)
Succ 0 // alias: Succ -> λn.λf.λx.f (n f x)
= (λn.λf.λx.f (n f x)) 0 // beta: λn.λf.λx.f (n f x) -> f (n f x)[n := 0]
= λf.λx.f (0 f x) // alias: 0 -> λs.λz.z
= λf.λx.f ((λs.λz.z) f x) // beta: λs.λz.z -> z[s := f, z := x] = x
= λf.λx.f x // alpha: f -> s, x -> z
= λs.λz.s z // 1

Plus

加法对于 2 + 3 我们可以理解为：对 3 调用 2 次后继函数 Succ，于是我们可以定义 Plus

// 解释一下: a, b 都是丘奇数, 将 Succ 和 b 应用于 a
// 相当于在 b 的 基础上, 调用了 a 次 Succ 函数
// 举个例子: 2 Succ 3 = (λs.λz.s (s z)) Succ 3 = Succ (Succ 3)
Plus := λa.λb.a S b // alias: S -> λn.λf.λx.f (n f x)
= λa.λb.a (λn.λf.λx.f (n f x)) b // beta: f (n f x)[ n := b]
= λa.λb.a (λf.λx.f (b f x)) // lambda lifting: https://en.wikipedia.org/wiki/Lambda_lifting
= λa.λb.λf.λx.a f (b f x) // alpha: a -> m, n -> n
= λm.λn.λf.λx.m f (n f x)
Plus 2 3 // alias: PLUS -> λm.λn.λf.λx.m f (n f x)
= (λm.λn.λf.λx.m f (n f x)) 2 3 // beta: m f (n f x)[m := 2, n := 3]
= λf.λx.2 f (3 f x) // alias: 2 -> λs.λz.s (s z)
= λf.λx.(λs.λz.s (s z)) f (3 f x) // beta: s (s z)[s := f]
= λf.λx.(λz.f (f z)) (3 f x) // beta: f (f z)[ z := (3 f x)]
= λf.λx.f (f (3 f x)) // alias: 3 -> λs.λz.s (s (s z))
= λf.λx.f (f ((λs.λz.s (s (s z))) f x)) // (λs.λz.s (s (s z))) f x -> s (s (s z)))[ s := f, z := x]
= λf.λx.f (f (f (f (f x)) // alpha: f -> s, x -> z
= λs.λz.s (s (s (s (s z))
= 5

对于减法，乘法，除法等其他运算，这里不详细展开，只列出其定义。其中除法的定义非常复杂，原因是除法的实现其实是通过递归不断的去逼近寻找到符合条件的值。这里面有递归，有 IsZero 的判定式，有减法，其中递归还要用到 Y 组合子，下文会讲到。

Pred := λn.λf.λx. n (λg.λh. h (g f)) (λu. x) (λu. u) // 前驱
Succ := λn f x.f (n f x) // 后继
Plus := λm.λn.λf.λx.m f (n f x) // 加法
Mult := λm.λn.λf.λx.m (n f) x // 乘法
Minus := λm.λn.n PRED m
// 很长，用 \ 代替 λ 符号
Div := (\n.((\f.(\x.x x) (\x.f (x x))) (\c.\n.\m.\f.\x.(\d.(\n.n (\x.(\a.\b.b)) (\a.\b.a)) d ((\f.\x.x) f x) (f (c d m f x))) ((\m.\n.n (\n.\f.\x.n (\g.\h.h (g f)) (\u.x) (\u.u)) m) n m))) ((\n.\f.\x. f (n f x)) n))

Predicates

Predicate 是返回布尔值的函数，我们暂且叫作判定式。

IsZero

判断是否等于 0

IsZero = λn.n (λx.False) True
IsZero Zero // alias: IsZero -> λn.n (λx.False) True
= (λn.n (λx.False) True) Zero // beta: n[ n:= Zero]
= Zero (λx.False) True // alias: Zero -> (λs.λz.z)
= (λs.λz.z) (λx.False) True // beta: [s := (λx.False), z := True]
= True

EQ & LEQ

比较数字大小，配合 Not, And 等逻辑运算符可以很容易的得到大于, 小于的表示方法

EQ := λm.λn.And (LEQ m n) (LEQ n m) // 等于
LEQ := λm.λn.IsZero (Minus m n) // 小于等于

Church pairs

丘奇编码中列表是通过二元组不断嵌套来表示的。这很像链表，每个二元组都可以用来表示一个链表节点。二元组的第一个元素是链表头结点，第二个元素则是另一个二元组 p，p 的第一个元素则是链表的第二个节点，p 的第二个元素又是下一个二元组 q, 以此类推...
其中二元组的定义和访问操作定义是这样的：

Pair := λx.λy.λz.z x y
First := λp.p (λx.λy.x) // 访问第一个元素
Second := λp.p (λx.λy.y) // 访问第二个元素
First (Pair 0 1) // alias: Pair -> λx.λy.λz.z x y
= First (λx.λy.λz.z x y 0 1) // beta: (z x y)[x := 0, y:= 1]
= First (λz.z 0 1) // alias: First -> λp.p (λx.λy.x)
= (λp.p (λx.λy.x)) (λz.z 0 1) // beta: p[p := (λz.z 0 1)]
= (λz.z 0 1) (λx.λy.x) // beta: z[z := (λx.λy.x)]
= (λx.λy.x) 0 1 // beta: x[x := 0, y := 1]
= 0

List encoding

有了 Pair 以后，列表的定义有很多种，维基百科上就有四种。这里我们选其中一种来看一下。其中 Cons 表示构造一个节点，Nil 表示空节点。

Cons := Pair
Head := First // 访问节点的值
Tail := Second // 访问下一个节点
Nil  := Pair True True
IsNil := λl.l (λh.λt.λd.False) True
Cons 1 (Cons 2 (Cons 3 Nil)) // (1, (2, (3, nil)))

Y combinator

我们还需要一种方式来表示递归，递归和循环等价，有了递归就有了循环。

递归的含义是「函数直接或间接的调用自身」，在编程语言中，函数要调用自身就要持有一个「自身的引用」，这个引用就是函数名。

但是在 lambda 演算中，所有函数都是匿名函数，那么如何引用自身？这需要用到 Y 组合子。

Y Combinator 是由 Haskell B. Curry 发现的。它用 λ 表达式表示的话长这样 λf.λx.(f(x x))(λx.(f(x x))).

Y 组合子用于计算高阶函数的不动点，这使得一个匿名函数可以包装成高阶函数后通过 Y 组合子得到自身，之后再调用自身来实现递归。

Fixed-point

函数 f 的不动点是将函数应用在输入值 x 时，会传回与输入值相同的值，使得 f(x) = x。

例如，0 和 1 是函数 f(x) = x^2 的不动点，因为 0^2 = 0 而 1^2 = 1。鉴于一阶函数（在简单值比如整数上的函数）的不动点是个一阶值，高阶函数 f 的不动点是另一个函数 g 使得 f(g) = g。Y 组合子可以计算出这个不动点 g，那么 g = y(f)，将 g 代入我们可以得到 y(f) = f(y(f))。

Y 组合子并不是唯一的不动点组合子，实际上有无限多个不动点组合子，另一个比较著名的是 Turing combinator

Y combinator in JavaScript

// 1.
// 一个朴素的计算阶乘的函数 fact
// 如果它是一个匿名函数，没有名字，那么如何递归调用自身？
let fact = function (n) {
  return n < 2 ? 1 : n * fact(n - 1)
};

// 2.
// 于是我们将它改成匿名函数，现在我们无法通过函数名去拿到关于自身的引用
// 我们可以包装一层, 变成高阶函数, 让外部传入一个计算阶乘的 f 函数进来
// 这样一来, 递归关于自身的引用就变成了对参数的引用
/* let fact0 = */ (function (f) {
  return function (n) {
    return n < 2 ? 1 : n * f(n - 1)
  }
});

// 3.
// 现在变成了一个高阶函数. 我们知道 f 是一个计算阶乘的函数,
// 于是我们就可以把最开始的那个阶乘函数 fact 传进来
fact = (function (f) {
  return function (n) {
    return n < 2 ? 1 : n * f(n - 1)
  }
})(function fact(n) {
  return n < 2 ? 1 : n * fact(n - 1)
});

// 4.
// 当然现在实参这里仍然保持了对自身的引用, 和第 2 步同样的方式
// 包装成高阶函数, 我们暂时把这个高阶函数叫作 fact0
// fact0 本身接受一个计算阶乘的函数, 返回一个计算阶乘的函数(有点绕口)
fact = (function (f) {
  return function (n) {
    return n < 2 ? 1 : n * f(n - 1)
  }
})(function (f) {
  return function (n) {
    return n < 2 ? 1 : n * f(n - 1)
  }
});

// 5.
// 这里传进来的形参 f 是高阶函数 fact0, fact0 是个高阶函数
// 所以原本的 f(n - 1) 调用方式需要修改成 f(?)(n - 1), 这里的 ? 表示要传一个函数
fact = (function (f) {
  return function (n) {
    // 回头看 fact0 的定义: fact0 本身接受一个计算阶乘的函数, 返回一个计算阶乘的函数
    // 这里进来的 f 是 fact0, 而 fact0 本身就可以用来计算阶乘
    // 于是我们就可以得到 f(?)(n - 1) -> f(fact0)(n - 1) -> f(f)(n - 1)
    return n < 2 ? 1 : n * f(f)(n - 1)
  }
})(function (f) {
  return function (n) {
    // 我们再来看这里, 在上面我们通过 f(f) 调用, 所以这里的形参 f 也是 fact0
    // 同样的做法, 我们将 f(n - 1) 修改成了 f(f)(n - 1)
    return n < 2 ? 1 : n * f(f)(n - 1)
  }
});
// 到这里, 这个 fact 已经可以运行了, 可以将代码贴到 devtools console 里运行一下试试

// 6.
// 接下来, 我们发现前面的代码有点冗余, 两个部分的代码完全一模一样,
// 所以我们可以将相同的部分提取出来, 提取的方式就是通过再包装一层, 将相同的部分变成参数 x
fact = (function (x) {
  return x(x)
})(function (f) {
  return function (n) {
    return n < 2 ? 1 : n * f(f)(n - 1)
  }
});

// 7.
// 我们的目的是要提取出一个公共的计算不动点的函数, 但现在阶乘那部分的代码是写死在里面的,
// 这部分逻辑应该是要是由外部来编写的, 所以我们需要提取一下这个部分
// 但显然你不想让每个人用不动点组合子的人都去写一个 f(f) 这样的一个奇怪的东西, 所以我们先提取 f(f)
// 方法是包装成 IIFE, g 作为形参, f(f) 作为实参传进去
fact = (function (x) {
  return x(x)
})(function (f) {
  return (function (g) {
    return function (n) {
      return n < 2 ? 1 : n * g(n - 1)
    }
  })(f(f))
});

// 8.
// 现在我们观察 IIFE 这部分, 这不就是我们前面写的 fact0 吗? 只不过参数名变成了 g
// 我们可以提取出去, 依然是包装成 IIFE 函数, 让它变成参数传进来
fact = (function (h) {
  return (function (x) {
    return x(x)
  })(function (f) {
    return h(f(f))
  })
})(function (g) {
  return function (n) {
    return n < 2 ? 1 : n * g(n - 1)
  }
});

// 9.
// 我们将实参以外的部分提取出来, 改个参数名称
// 我们观察 x(x) 是什么, 对实参部分进行调用后, 我们得到的是实际是 f(x(x))
// 即 f(x(x)) 和 x(x) 等价, 回顾前面不动点的定义: 高阶函数 f 的不动点是另一个函数 g 使得 f(g) = g
// 因此 x(x) 其实就是形参 f 的不动点
(function (f) {
  return (function (x) {
    return x(x) // 调用后, 这里得到的实际是 f(x(x))
  })(function (x) {
    return f(x(x))
  })
});

// 10. 由于等价, 因此我们将 x(x) 修改为 f(x(x)), 就得到了我们的 y 组合子
let y = (function (f) {
  return (function (x) {
    return f(x(x))
  })(function (x) {
    return f(x(x))
  })
});

// 11.
// 但是, 你把以下这段代码贴到 console 里面去执行, 发现会爆栈.
// 原因是 y 组合子内部 f(x(x)) 这里其实是个无限递归的结构, 而 js 本身又是立即求值的语言
// 不管你消不消费这个值, 他都会先求值, 这就导致这个递归无法停止导致爆栈.
y(function (f) {
  return function (n) {
    return n < 2 ? 1 : n * f(n - 1)
  }
})(5)

// 12. 我们需要一些手段让它只有在需要的时候才去求值, 方法就是在求值的地方包装一个函数
// 我们把这种函数叫作 thunk. e.g. `foo(1 + 2) -> foo(() => 1 + 2)`,
// 这里的 `() => 1 + 2` 就是个 thunk
// 下面会介绍两种包装成 thunk 的方法
// 第一种:
y = (function (f) {
  return (function (x) {
    return f(x(x))
  })(function (x) {
    return (v) => f(x(x))(v)
  })
});
// 第二种也叫 Z combinator
let z = (function (f) {
  return (function (x) {
    return f(v => x(x)(v))
  })(function (x) {
    return f(v => x(x)(v))
  })
});

// 最终代码
z((function (f) {
  return function (n) {
    return n < 2 ? 1 : n * f(n - 1)
  }
}))(5)

1/13

1, 2, 3.map(x => x + 1)

用上面的知识来表达 [1, 2, 3].map(x => x + 1)

const If = p => a => b => p(a)(b)
const True = a => b => a
const False = a => b => b
const One = s => z => s(z);
const Two = s => z => s(s(z));
const Three = s => z => s(s(s(z)));
const Succ = n => f => x => f(n(f)(x))
const Plus = m => n => f => x => m(f)(n(f)(x))
// z combinator
const z = f => (x => f(v => x(x)(v)))(x => f(v => x(x)(v)))
const Pair = x => y => z => z(x)(y)
const First = p => p(x => y => x)
const Second = p => p(x => y => y)
// List
const Cons = Pair
const Head = First
const Tail = Second
const Nil = False
const isNil = l => l(h => t => d => False)(True)
const Map = z(map => list => f => {
  // 由于 js 立即求值会爆栈, 这里包装一下
  return If(isNil(list))((/* thunk */) => Nil)(
    (/* thunk */) => Cons(f(Head(list)))(map(Tail(list))(f)(/* Map 返回的实际上是个 thunk, 这里手动调用一次 */))
  )
})
// [1, 2, 3]
const input = Cons(One)(Cons(Two)(Cons(Three)(Nil)))
const AddOne = x => Plus(x)(One)
// [2, 3, 4]
const result = Map(input)(AddOne)(/* Map 返回的实际上是个 thunk, 这里手动调用一次 */)
console.log('Input:', convertNumList(input))
console.log('Result:', convertNumList(result))
// Helpers
function convertNumList(listNode) {
  let current = listNode
  const res = []
  while (isNil(current)(false)(true)) {
    res.push(convert(Head(current)))
    current = Tail(current)
  }
  return res
}
function s(n) {
  return n + 1
}
function convert(f) {
  return f(s)(0)
}